Binary Data Storage and Manipulation
Demonstrating Physical Representation and Implementation |
|
|
::Binary Addition::
Since the function of our project is to add two numbers together, we will now explain how this is done by using logic gates.
Addition of binary numbers is really quite simple, because there are only two numbers, 0 and 1.
Simple arithmetic rules apply, just as for decimal numbers, when adding binary numbers.
For example, 0 plus 0 equals 0, 1 plus 0 equals 1, etc. To perform this function, a device called a half-adder is used. A half adder is the circuitry necessary to add two binary digits together.
A half-adder is derrived from logic gates.
A half-adder, as it's name suggests, is only half of the solution. A half-adder does not address the issue of 1 + 1. 1 + 1 needs to equal 0 and carry the 1.
This issue is addressed by linking two half-adders together to build a full adder that deals with carry digits. While there are many ways to derrive a full-adder, this is the method we have chosen is shown below.
In order to add multi-bit numbers, e.g. 1100 0011 + 1110 0011, it is necessary to "chain" several full adders together. This is discussed more in the next section, Project Details.
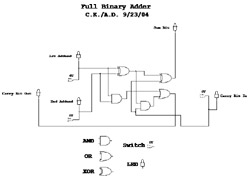
Some photos of our implementation of this schematic in it's various states...








|
|
|